Day 3（还是我们熟悉的钟皓曦大佬）

讲了神奇的组合数问题（据说各个网站的组合数问题都是钟皓曦出的，所以他说都是好题）

组合数需要用到下面两个原理和两个神奇的东西

加法原理：具有性质A的事件有m个，

具有性质B的事件有n个,则具有性质A或者性质B的事件有m+n个

乘法原理：具有性质A的事件有m个，

具有性质B的事件有n个,则具有性质A以及性质B的事件有m*n个

组合：从n个元素中选取r个元素，

当不计顺序时，其方案数为C（n，r）=n！/【r！*（n-r）！】

排列：从n个元素中选取r个元素，

当考虑顺序时，其方案数为P（n，r）=n！/（n-r）！

 这里的组合数满足一些性质:

1.有 n个不同元素，从中选r个，但是选择的元素不能相邻，其方案数为C（n-r+1,r）（至于这里的证明我也十分的迷茫，就先不证了，大家先凑合着看）；

2.有n个不同元素，从中选r个，但是每个可以选多次，则其方案数为C(n+r-1,r)

3.其他的性质：

• C(n+m,n)=C(n+m,m)
• C(n,m)=C(n-1,m-1)+C(n-1,m)
• C(n+r+1,r)=C(n+r,r)+C(n+r-1,r-1)+C(n+r-2,r-2)+....+C(n,0)
• C(n,l)C(l,r)=C(n,r)C(n-r,l-r)
• C(n,0)+C(n,1)+.....+C(n,n)=2ⁿ
• C(n,0)-C(n,1)+C(n,2)-...=0
• C(r,r)+C(r+1,r)+...+C(n,r)=C(n+1,r+1)

 没错，就这么多性质，且看且珍惜QAQ

容斥原理

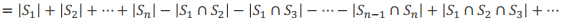
第二类斯特林数

n个有区别的球放到m个相同的盒子中要求没有空盒的方案数

记为S(n,m)

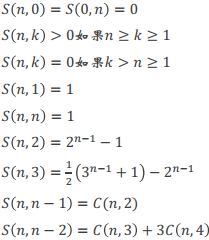
（↗这是一些神奇的栗子例子）

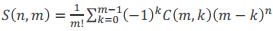
（↗这貌似是通式）

卡特兰数

将凸n边形划分为三角形的方案数

记为C（n）

则C（n）=C（2）C（n）+C（3）C（n-1）+···+C（n）C（2）

C（n+1）=1/n C（2n-2，n-1）（这个C是组合数）

（↗这貌似是通式）

剩下的便是一些例题，以后会再整理